Skip to contents

Classes and methods for min-cost flow solutions

Ben B. Hansen, Josh Errickson, Mark Fredrickson, Adam Rauh and Peter Solenberger

2024-11-08

Source: vignettes/MCFSolutions.Rmd
MCFSolutions.Rmd

Overview

Optmatch finds optimal matches by translating them to min-cost flow problems (Rosenbaum, 1991, JRSS-B; Hansen and Klopfer, 2006, JCGS), relying on a min-cost flow solver that works by dual ascent. Through 2018 (version 0.9*), no attempt was made to store the dual problem solution found by this solver; accordingly, it was not possible to use that solution as a starting value for related matching problems. This document lays out a roadmap for “daylighting” the min-cost flow material, i.e. making it accessible to the R user, for warm starts and supplementary calculations.

Proximate goals

  1. When solver saw a discretized version of the distance, check whether solution is optimal for matching problem w/ double precision distance (by checking whether primal solution and back-transformed dual solution stand in CS relation to one another). (Cf. issue 160.)
  2. Warm starts for MCF problems deriving from same double-precision distance but w/ a different discretization. (Cf. issue 76.)
  3. Use dual solution to one problem as warm start for another problem with same arcs, arc costs as in original problem but adding new arcs (between existing nodes).
  4. Use dual solution to one problem as warm start for another problem with same arcs and arc costs, but adding new “downstream” nodes and new arcs connecting them to existing “upstream” nodes.

Maybe-later goals

  • Flexibly combine subproblem solutions (e.g., distributing subproblems across different cores before combining).
  • Merge dual solutions of distinct subproblems, arriving at a possible starting value for a combined subproblem.
  • supercede optmatch s3 class, methods with an S4 class, methods.
  • Use the dual solution as a basis for computing maxErr / exceedance.

Classes

Subproblems / SubProbInfo

An SubProbInfo is an S4-typed data frame bearing information about (sub)problems passed to the solver, and their translation to and from units acceptable to the solver. Columns:

  • groups, character (which subproblem?);
  • flipped, logical (do upstream nodes of MCF representation correspond to columns of match distance matrix, as opposed to rows, the default?);
  • hashed_dist, character (hashed ID for a double precision distance);
  • resolution, double (grid-width for discretization of distances & node prices before rounding and handing off to solver);
  • lagrangian_value, numeric (as determined by back-transformed node prices, arc costs and arc flows);
  • dual_value, numeric (as determined by back-transformed node prices and arc costs);
  • feasible, logical;
  • exceedance, double (the legacy criterion regret calculation).

Rules/conventions:

  • this is just a selective record of subproblem specs.
  • This type’s validity checker should be fast, eschewing expensive operations.
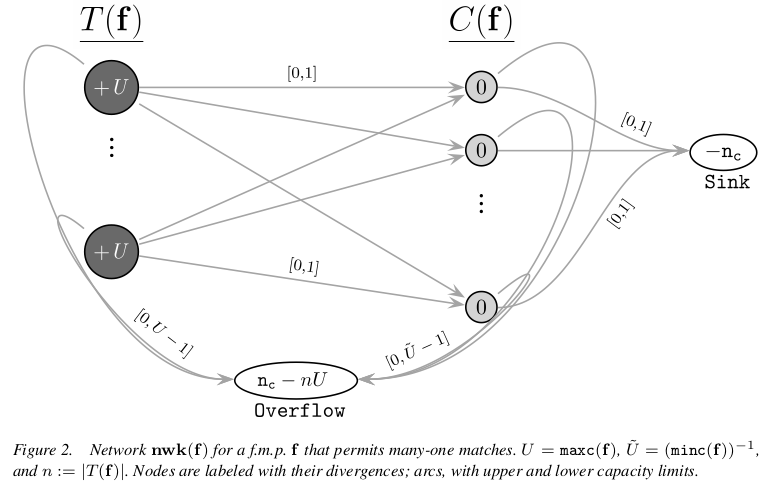
  • feasible encodes whether the flow-price pair was found to be in a complementary slackness relationship, prior to backtransformation of distances & prices (if applicable). In other words, feasible==FALSE indicates that the subproblem imposed infeasible matching constraints.
  • “Upstream” nodes are those to the left in the below diagram (Fig. 2 of Hansen & Klopfer, 2006). Ordinarily they’ll correspond to “the treatment group”, i.e. the group indexed by rows of the distance matrix helping to determine the matching problem, but in some situations rows and columns are flipped before being passed to the solver, so that upstream nodes would correspond to columns and downstream nodes to rows.
Fig. 2 of Hansen & Klopfer, 2006, JCGS
Fig. 2 of Hansen & Klopfer, 2006, JCGS

NodeInfo & subclasses

A NodeInfo is an S4-typed data frame bearing a non-null row.names attribute and columns:

  • name, character;
  • price, double or integer (node prices);
  • upstream_not_down, logical (node type indicator, see below);
  • supply, integer;
  • groups, factor (optional; name of a subproblem); and
  • … (hold open the possibility of additional columns for subclasses).

Rules/conventions:

  • This document terms “node labels” the row names of a NodeInfo table.
  • Multiple subproblems’ node information can be combined into a single NodeInfo object.
  • Ordinarily a NodeInfo’s name column and its node labels are the same. The reason for the presence of both is to avoid duplication among node labels, which might otherwise occur when a NodeInfo arises by concatenation of solutions to distinct matching problems (which so happened to involve distinct units that shared names).
  • Within levels of groups, values of name should be unique. (Presently the validity checker only looks for this when groups has a single level, in the interests of avoiding slowdowns when combining NodeInfo’s.)
  • Coding of node types in upstream_not_down column: TRUE ~ upstream, i.e. “T(f)” nodes in Fig. 2 of H.&K. ’06, FALSE ~ downstream or “C(f)” nodes in H.&K. ’06 Fig. 2; NA ~ bookkeeping nodes, e.g. “Overflow” or “Sink” in H.&K. ’06 Fig. 2.
  • A node’s price can be NA_real_, but only if upstream_not_down=FALSE. See also Rules/conventions pertaining to MCFSolutions objects, below.
  • This type’s validity checker should be fast, eschewing expensive operations.
  • If the solver operated on a transformation of the distance, it’s the correspondingly back-transformed node prices that are stored in the NodeInfo.

ArcInfo

An ArcInfo has 2 slots:

  • @matches, data frame with columns
    • groups, factor,
    • upstream, factor,
    • downstream, factor;
  • @bookkeeping, data frame with columns
    • groups, factor,
    • start, factor,
    • end, factor,
    • flow, integer (nonnegative),
    • capacity, integer (nonnegative).

Rules/conventions:

  • In terms of the network flow solution, presence of a row in @matches encodes a corresponding flow of 1; absence encodes flow 0. (So having the row means its upstream/start node and downstream/end nodes were matched, absence means not matched.)
  • The factors upstream, downstream, start and end all have the same levels().
  • Arcs involving bookkeeping nodes have lower capacity 0, upper capacity capacity. Their flow values must fall in this range (inclusive of endpoints).
  • This type’s validity checker should be fast, eschewing expensive operations.
  • The @bookkeeping d.f. must have a row for each of the bookkeeping arcs of the problem.
  • Each (groups, upstream) pair must appear as a (groups, name) pair in the NodeInfo table, with upstream_not_down==TRUE; each (groups, downstream) pair must appear as a (groups, name) NodeInfo pair, with upstream_not_down==FALSE.
  • Similarly a (groups, start) or (groups, end) pair carried in this table must have in the NodeInfo table a corresponding (groups, name) entry.

Primal-dual solution pairs (MCFSolutions)

In practice, current plans call only for passing dual solutions (arrays of node prices), not also primal solutions (flow vectors), back to the solver. But in principle the relax4f solver could accommodate dual-primal pairs as start values, at the cost of rejiggering our interactions; see comments to issue 162. Also assessing CS requires the combo of a primal and dual solution. So we’ll save both of them, as an S4 object.

Slots for class MCFSolutions:

  • subproblems, a “SubProbInfo” object (see above);
  • nodes, a NodeInfo object (see above); and
  • arcs, a ArcInfo object (see above).

Rules/conventions:

  • The node-identifying columns of @arcs all have precisely the same collection of levels (as is enforced by the ArcInfo validity checker). In addition, they coincide with row.names(.@nodes). The latter to be enforced by MCFSolutions’s validity check.
  • The @nodes table has to have a groups column.
  • The nodes table will include nodes that don’t correspond to any unit described in the corresponding match vector: bookkeeping nodes; potentially also nodes for units that have been filtered out the match vector.
  • It may also include nodes that were not a part of the MCF problem presented to the solver. (B/c e.g. they represent subjects that were were excluded prior to matching, or their subproblem was found to be infeasible prior to being sent to the solver, they’re part of some other subproblem than the one(s) currently under consideration.) In this case the corresponding @node$price value may be NA_real_ and references to them will not appear in corresponding ArcInfo tables.
  • Distinct matchable units must not share node labels (values of row.names(@nodes)).
  • Nor should bookkeeping nodes for distinct subproblems.
  • For subjects not appearing in a subproblem that was sent to the solver (b/c they were removed from the subproblem first, or b/c their subproblem was found to be infeasible), we won’t have a record of their subgroup or treatment status. OTOH everyone matched will have been processed in this way, and for all such subjects the @nodes table carries an explicit record of their subgroup, which @subproblems and @nodes combine to give row/column or treatment/control status via
ifelse(with(object@subproblems, flipped[match(object@nodes$groups,groups)]),
       !object@nodes$upstream_not_down,
       object@nodes$upstream_not_down)
  • Checking validity for such an object may be moderately expensive when the object is large, as it calls for cross-comparison of constituent objects. So e.g. c() should not routinely check validity on its result; rather the check should be applied to smaller objects.
  • Hold @.Data, @names and @levels slots for likely future use; see below notes re future Optmatch S4 class.

Subtypes for specific matching problems

Different kinds of matching problem have different bookkeeping nodes, implicit arc capacity constraints etc. Encode all this by declaring appropriate subclasses of MCFSolutions().

FullmatchMCFSolutions

A type extending MCFSolutions(), w/ characteristics:

  • in @nodes, exactly 2 node labels per subproblem s.t. is.na(upstream_not_down): a string beginning with “(_Sink_)” and another beginning with “(_End_)”;
  • in @nodes, also each of those appears exactly once per subproblem;
  • in @nodes, each node with upstream_not_down == TRUE has positive supply;
  • in @nodes, each node with upstream_not_down == FALSE has supply==0;
  • in @nodes, each node with is.na(upstream_not_down) has nonpositive supply;
  • in @arcs@bookkeeping, each node with !is.na(upstream_not_down) appears as the start of an arc that has end node (a string beginning w/) (_End_);
  • in @arcs@bookkeeping, each node with upstream_not_down == FALSE appears as the start of an arc that has end node named by a string beginning with (_Sink_).

Return value of fullmatch / pairmatch (*ptmatch)

Immediate plan

Return an object bearing S3 class “optmatch”, as we did before these changes. Embed an MCFSolutions into it as an attribute.

Final solution

Return object of a new S4 class, Optmatch, inheriting from factor as well as from MCFSolutions.

Methods & Functions

  • as.optmatch()/as.factor() for MCFSolutions objects
  • node.labels(),node.labels<- for MCFSolutions objects (to pull /set row.names(@nodes))
  • getMCFSolution(): extractor for optmatch objects (& later for Optmatch objects)
  • c() for MCFSolutions: rbind()s the various constituent data frames, enforcing req’s that subproblems have distinct names, de-duping bookkeeping nodes and enforcing requirement that non-bookkeeping nodes’ names be distinct.
  • addArcs() for MCFSolutions objects
  • addNodes() for MCFSolutions objects